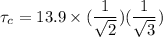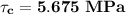Answer:
Step-by-step explanation:
Given that:
The direction of the applied tensile stress =[001]
direction of the slip plane = [
 01]
01]
normal to the slip plane = [111]
Now, the first thing to do is to calculate the angle between the tensile stress and the slip by using the formula:
![cos \lambda = \Big [(d_1d_2+e_1e_2+f_1f_2)/(√((d_1^2+e_1^2+f_1^2)+(d_2^2+e_2^2+f_2^2) )) \Big]](https://img.qammunity.org/2022/formulas/engineering/college/zeros7dffaf0xbs877ykyhodp1lzzhyb5i.png)
where;
![[d_1\ e_1 \ f_1]](https://img.qammunity.org/2022/formulas/engineering/college/1l55w8xfxi4lwcomnpc1pzgbddauws4cd1.png) = directional indices for tensile stress
= directional indices for tensile stress
![[d_2 \ e_2 \ f_2]](https://img.qammunity.org/2022/formulas/engineering/college/5eozaiyvokypez04phub0rnhh8e3i0hkxm.png) = slip direction
= slip direction
replacing their values;
i.e
 = 0 ,
= 0 ,
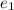 = 0
= 0
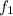 = 1 &
= 1 &
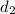 = -1 ,
= -1 ,
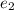 = 0 ,
= 0 ,
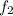 = 1
= 1
![cos \lambda = \Big [((0* -1)+(0* 0) + (1* 1) )/(√((0^2+0^2+1^2)+((-1)^2+0^2+1^2) )) \Big]](https://img.qammunity.org/2022/formulas/engineering/college/qczzms9irvnk2hnh8jl51ednctnm8woi2k.png)
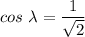
Also, to find the angle
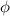 between the stress [001] & normal slip plane [111]
between the stress [001] & normal slip plane [111]
Then;
![cos \ \phi = \Big [(d_1d_3+e_1e_3+f_1f_3)/(√((d_1^2+e_1^2+f_1^2)+(d_3^2+e_3^2+f_3^2) )) \Big]](https://img.qammunity.org/2022/formulas/engineering/college/fecfgc05lzpbwedepkbwtnpl0mq93e2g2y.png)
replacing their values;
i.e
 = 0 ,
= 0 ,
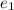 = 0
= 0
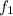 = 1 &
= 1 &
 = 1 ,
= 1 ,
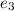 = 1 ,
= 1 ,
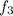 = 1
= 1
![cos \ \phi= \Big [ \frac{ (0 * 1)+(0 * 1)+(1 * 1)} {\sqrt {(0^2+0^2+1^2)+(1^2+1^2 +1^2)} } \Big]](https://img.qammunity.org/2022/formulas/engineering/college/46zjchugmqh58jdye96itpqx1pfsoraqaf.png)

However, the critical resolved SS(shear stress)
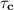 can be computed using the formula:
can be computed using the formula:
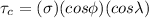
where;
applied tensile stress
 13.9 MPa
13.9 MPa
∴