Question

Please show the steps. and the answer

Answer 1

$321562.50

Explanation:

Exponential growth can be modeled by the formula
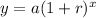`y = a(1+r)^(x)` , with y representing the final value, a being the starting value, r being the growth rate, and x being the number of time intervals passed.

To figure out the rate, we must use the values given from the months we have data of. Our starting value is 60,000 , ending value is 105,000 , and given that monthly sales are given, we can assume that sales grew exponentially each month. There were 4 years, or 48 months, that the store had to grow. Our formula is thus

`105000 = 60000(1+r)^(48)\\`

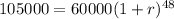
To solve for r, we can first divide both sides by 60,000 , then put each side to the power of 1/48, resulting in

`105000/60000 = (1+r)^(48)\\1.75 = (1+r)^(48)\\\\1.75^(1/48) = 1+r`

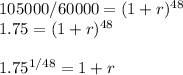
Since we know our rate, and there are 8 years/96 months between January 2005 and January 2013, we can make our starting value 105,000 , plug (1.75)^(1/48) for r and 96 for x in
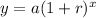`y = a(1+r)^(x)`, and go from there.

Our final value is then

`y = 105000(1.75^(1/48))^(96)\\y = 105000(1.75^(2))\\y = 321562.5`. We were able to turn 1.75^(1/48)^(96) into 1.75² using the exponent rule stating that x^y^z = x^(y*z)