Answer:
$321562.50
Explanation:
Exponential growth can be modeled by the formula
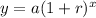 , with y representing the final value, a being the starting value, r being the growth rate, and x being the number of time intervals passed.
, with y representing the final value, a being the starting value, r being the growth rate, and x being the number of time intervals passed.
To figure out the rate, we must use the values given from the months we have data of. Our starting value is 60,000 , ending value is 105,000 , and given that monthly sales are given, we can assume that sales grew exponentially each month. There were 4 years, or 48 months, that the store had to grow. Our formula is thus
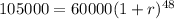
To solve for r, we can first divide both sides by 60,000 , then put each side to the power of 1/48, resulting in
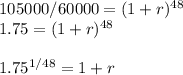
Since we know our rate, and there are 8 years/96 months between January 2005 and January 2013, we can make our starting value 105,000 , plug (1.75)^(1/48) for r and 96 for x in
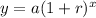 , and go from there.
, and go from there.
Our final value is then
 . We were able to turn 1.75^(1/48)^(96) into 1.75² using the exponent rule stating that x^y^z = x^(y*z)
. We were able to turn 1.75^(1/48)^(96) into 1.75² using the exponent rule stating that x^y^z = x^(y*z)