Answer:
I. x = 14.115 and y = 9.115
II. x = 0.885 and y = -4.115
Explanation:
- Let the two numbers be x and y respectively.
Translating the word problem, we have;
x - y = 5 ......equation 1
x² + y² = 100 ...... equation 2
x = y + 5 ...... equation 3
Substituting eqn 3 into eqn 2, we have;
(y + 5)² + y² = 100
Simplifying further by opening the bracket, we have;
(y + 5)(y + 5) + y² = 100
y² + 5y + 5y + 25 + y² = 100
y² + 10y + 25 + y² = 100
2y² + 10y + 25 = 100
2y² + 10y + 25 - 100 = 0
2y² + 10y - 75 = 0
To find the roots of the quadratic equation, we would use the quadratic formula;
Note: the standard form of a quadratic equation is ax² + bx + c = 0
a = 2, b = 10 and c = -75
The quadratic equation formula is;
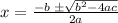
Substituting into the formula, we have;
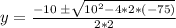
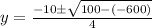
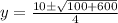
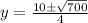
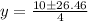

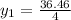
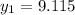
Or
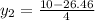
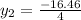
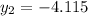
Next, we would find the value of x;
x = y + 5
When y = 9.115
x = 9.115 + 5
x = 14.115
When y = -4.115
x = -4.115 + 5
x = 0.885
Check:
x - y = 5
14.115 - 9.115 = 5