Answer:
The length of QR is approximately 18.3 cm
Explanation:
The given parameters are;
The length of the side PR = 23 cm
The length of the side PQ = 22 cm
The measure of the angle QPR = 48°
By cosine rule, we have;

Plugging in the values gives;
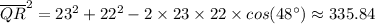
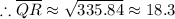
The length of QR ≈ 18.3 cm