Question

PQR is a triangle. PR= 23cm, PQ= 22cm and angle QPR= 48 degrees. Calculate length of QR.

Answer 1

The length of QR is approximately 18.3 cm

Explanation:

The given parameters are;

The length of the side PR = 23 cm

The length of the side PQ = 22 cm

The measure of the angle QPR = 48°

By cosine rule, we have;

`\overline{QR}^2 = \overline{PR}^2 + \overline{PQ}^2 - 2 * \overline{PR} * \overline{PQ} * cos(\angle QPR)`

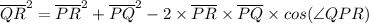
Plugging in the values gives;

`\overline{QR}^2 = 23^2 + 22^2 - 2 * 23 * 22* cos(48^(\circ)) \approx 335.84`

`\therefore \overline{QR} \approx √(335.84) \approx 18.3`

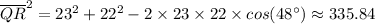
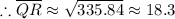
The length of QR ≈ 18.3 cm