Question

The width of a rectangle is 3 inches less than its length, and the area is 88 square inches. What are the length and width of the rectangle?

Answer 1

`\large{ \tt{❃ \: EXPLANATION}} :`

• Remember - The formula to find out the area of a rectangle is l × w where l = length & w = width.

• Let the length of a rectangle be ' l ' . We're provided - Width ( w ) = l - 3 & area of rectangle ( A ) = 88 square inches. We're asked to find out the length and width of the rectangle. Let's begin !

`\large{ \tt{❁ \: SOLUTION}} :`

`\large{ \tt{♡ \: AREA \: OF \: RECTANGLE \: ( \: A \: ) = \bf l * w}}`

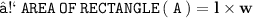
• Plug the values and then simplify :

`\large{ \text{⟶ \: 88 = l(l - 3)}}`

`\large{ \bf{⟶ \: 88 = {l}^(2) - 3 l}}`

`\large{ \bf{⟶ {l}^(2) - 3l = 88 }}`

`\large{ \bf{⟶ \: {l}^(2) - 3l - 88 = 0}}`

`\large{ \bf{ ⟶{l}^(2) - (11 - 8)l - 88 = 0}}`

`\large{ \bf{⟶ {l}^(2) - 11l + 8l - 88 = 0}}`

`\large{ \bf{⟶ \: l(l - 11) + 8(l - 11) = 0}}`

`\large{ \bf{⟶ \: (l - 11)(l + 8) = 0}}`

• Either :

`\large{ \bf{⟶ \: l - 11 = 0}}`

`\large{ \bf{⟶l = 11 \: in}}`

• Or :

`\large{ \bf{⟶l + 8 = 0}}`

`\large{ \bf{⟶l = - 8 \: in}}`

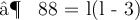
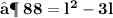
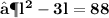
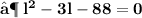
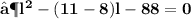
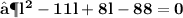
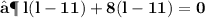
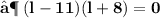
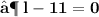
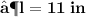
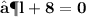
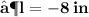
• We found out the two values of length of given rectangle [ i.e 11 in & 8 in ]. Since the length can't be in negative , we consider length of the rectangle as ' 11 in ' .

`\large{ \tt{❈ \: NOW, \: REPLACING \: VALUE}} :`

`\large{ \tt{⤑ \: Width(w) = l - 3 = 11 * 3 = \underline{ \tt{8 \: in}}}}`

`\underline{ \underline{ \large{ \tt{☄OUR \: FINAL \: ANSWER \: }}} }:`

• 
  `\large{ \boxed{\tt{Length = \underline{ 11 \: in}}}}`

• 
  `\large{ \boxed{ \tt{Width = \underline{8 \: in}}}}`

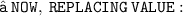
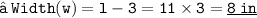
☂ Yippie! we're done!

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁