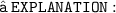
- Remember - The formula to find out the area of a rectangle is l × w where l = length & w = width.
- Let the length of a rectangle be ' l ' . We're provided - Width ( w ) = l - 3 & area of rectangle ( A ) = 88 square inches. We're asked to find out the length and width of the rectangle. Let's begin !

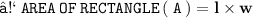
- Plug the values and then simplify :
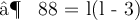
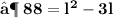
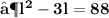
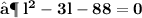

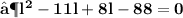
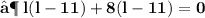
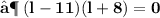
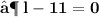
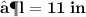
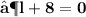
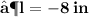
- We found out the two values of length of given rectangle [ i.e 11 in & 8 in ]. Since the length can't be in negative , we consider length of the rectangle as ' 11 in ' .


☂ Yippie! we're done!
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁