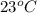Answer: The final temperature will be
Step-by-step explanation:
Calculating the heat released or absorbed for the process:
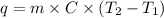
In a system, the total amount of heat released is equal to the total amount of heat absorbed.
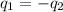
OR
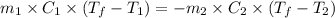 ......(1)
......(1)
where,
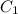 = specific heat of aluminium =
= specific heat of aluminium =
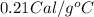
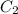 = heat capacity of water =
= heat capacity of water =
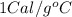
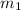 = mass of aluminium = 30. g
= mass of aluminium = 30. g
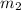 = mass of water = 50. g
= mass of water = 50. g
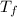 = final temperature of the system = ?
= final temperature of the system = ?
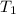 = initial temperature of aluminium =
= initial temperature of aluminium =
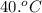
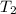 = initial temperature of the water =
= initial temperature of the water =
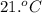
Putting values in equation 1, we get:
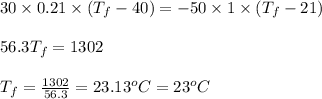
Hence, the final temperature will be