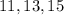Question

Find three consecutive odd integers such that the sum of the​ first, two times the second and three times the third is 82.

A) 6x + 8 = 82
B) 6x + 16 = 82
C) 3x + 3 = 82
D) 3x + 6 = 82

Answer 1

I think the answer is (A)

Answer 2

`11, 13, 15`

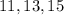
B) 6x + 16 = 82

Note: I just kept my wrong approach.

Explanation:

Let first define an odd integer.

Considering
`x\in\mathbb{Z}: 2k+1`,
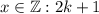`x` is an odd integer.

Now, three consecutive odd integers are
`a_1 = 2k+1` ,
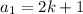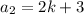`a_2 = 2k+3` and
`a_3 = 2k+5`

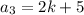
The sum of the​ first, two times the second and three times the third can be written as

`a_1 + 2a_2 + 3a_3 = 2k+1 + 2(2k+3)+3(2k+5)`

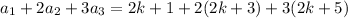
Expanding and simplifying

`2k+1 + 2(2k+3)+3(2k+5) = 2k+1 +4k+6+6k+15 = 12k+22`

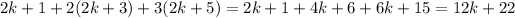
This is what I have done initially, but considering
`x` to be an odd integer, three consecutive integers can be written as

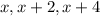`x, x+2, x+4` such that
`x\in\mathbb{Z}: 2k+1`

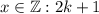
Therefore,

`x+2(x+2)+3(x+4)=82 \implies x+2x+4+3x+12 = 82 \implies 6x+16 = 82`

and
`6x+16 = 82 \implies 6x = 66 \implies x = 11`

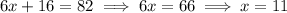
The three consecutive odd integers such that the sum of the​ first, two times the second and three times the third is 82 are
`11, 13, 15`