Answer:
You would be correct the GCF is
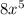 .
.
Step by Step Explanation:
So the GCF is basically a value that can go into or be factored out of two or more other numbers.
For instance, the greatest common factor of 10 and 20 is 10, since 10 is the greatest number that goes into 10 and 20 resulting in a integer.
Its a bit different with variables and exponents.
For instance, normally a number needs to be able to be divided nicely by the GCF. In exponents, the lowest exponent is the one you use.
If you had x^4 x^6 x^8, the GCF is x^4. It doesnt need to divide each exponent, but needs to be able to be subtracted by it,
You can think of it like how division and multiplication works with exponents.
With variables, it is similar to normal numbers.
The coefficent of the GCF must go into the coefifcent of the variables.
The variables also have to be the same, for instance x can never have a GCF of y.
So remembering this, lets find the GCF of your problem
We see the expoent of the first number is 7. The exponent of the other is 5.
Because we look at the lowest exponent as the GCF, the exponent 5 would be the GCF of the two values.
Then looking at the 8x and 24x, we know that 8x must be the GCF, since 8 equally divides between the 8 and 24, and they both have a x.
So combining the 5 exponent and the 8x:
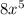
So this is your answer.