Question

Which are solutions of the equation x^2-16=0? Check all that apply.

Answer 1

x = 4

x = - 4

Explanation:

Method 1: Quadratic Formula

Ignore the A before the ±, it wouldn't let me type it correctly.

`x=\frac{-b±\sqrt{b^(2) -4ac} }{2a}`

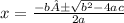
x² - 16 = 0

a = 1

b = 0

c = - 16

`x=\frac{-(0)±\sqrt{0^(2) -4((1)(-16))} }{2(1)}`

`x=(0±√(0 -4((1)(-16))) )/(2(1))`

`x=(0±√(0 +64) )/(2(1))`

`x=(0±√(64) )/(2)`

`x=(0±8 )/(2)`

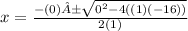
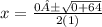
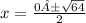
Two separate equations

One must have a + (positive) and the other will have a - (negative).

`x=(0+8 )/(2)`

`x=(8 )/(2)`

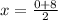
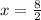
x = 8 ÷ 2

x = 4

`x=(-8 )/(2)`

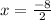
x = - 8 ÷ 2

x = - 4

Method 2: Factoring

x² - 16 = 0

(x - 4)(x + 4) = 0

Two separate equations

x - 4 = 0

x + 4 = 0

x - 4 = 0

x - 4 + 4 = 0 + 4

x = 4

x + 4 = 0

x + 4 - 4 = 0 - 4

x = - 4

Answer 2

+4, -4

Explanation:

There are only two solutions to this equation.

=> x^2 - 16 = 0

=> x^2 - 4^2 = 0

=> (x+4) (x-4) = 0 {According to a^2 - b^2 = (a+b) (a-b)}

=> x = 4, -4