Answer:
x = 4
x = - 4
Explanation:
Method 1: Quadratic Formula
Ignore the A before the ±, it wouldn't let me type it correctly.
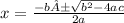
x² - 16 = 0
a = 1
b = 0
c = - 16
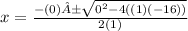
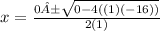
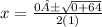
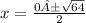
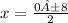
Two separate equations
One must have a + (positive) and the other will have a - (negative).
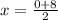
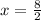
x = 8 ÷ 2
x = 4
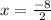
x = - 8 ÷ 2
x = - 4
Method 2: Factoring
x² - 16 = 0
(x - 4)(x + 4) = 0
Two separate equations
x - 4 = 0
x + 4 = 0
x - 4 = 0
x - 4 + 4 = 0 + 4
x = 4
x + 4 = 0
x + 4 - 4 = 0 - 4
x = - 4