Answer:
Q32) we have:
x² - Px + P = x(x - P) + P
but x² - Px + P is divisible of x - P
=> P must be divisible of x - P
=> P = 0
Q37) 3x² + Px + 54 = 0
a = 3 b = P c = 54
=> delta = b² - 4ac = P² - 648
because this equation have 2 solutions => delta > 0
=> P² - 648 > 0
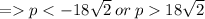
x1, x2 are 2 solutions of this equation
=> x1 = 2.x2
=> x1 - 2.x2 = 0
Using Viète theorem, we have:
x1 + x2 = -P/3
x1.x2 = 18
but x1 = 2.x2 => 3.x2= -P/3
2.x2² = 18
=> -9.x2 = P
x2² = 9 => x2 = 3 or - 3
=> P = 27 or - 27
Q47) because Px² + 2x³ + qx + c is divided by x+ 1 and x-2
=> P - 2 - q + c = 0
4P + 16 + 2q + c = 0
=> 3p + 3q = - 18
=> p + q = -6