Answer:
[C]
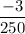
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
- Terms/Coefficients
- Factoring
- Functions
- Function Notation
- Conjugations
Calculus
- Limits
- Limit Rule [Variable Direct Substitution]:
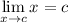
- Limit Property [Multiplied Constant]:
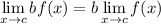
- Derivatives
- Definition of a Derivative:
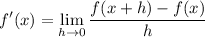
Explanation:
Step 1: Define
Identify
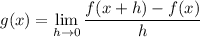
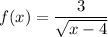
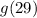
Step 2: Differentiate
- Substitute in function [Function g(x)]:
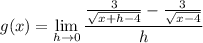
- Substitute in x [Function g(x)]:
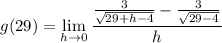
- Simplify:
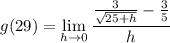
- Rewrite:
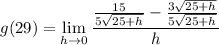
- [Subtraction] Combine like terms:
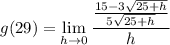
- Factor:
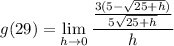
- Rewrite:
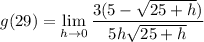
- Rewrite [Limit Property - Multiplied Constant]:
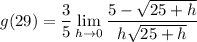
- Root Conjugation:
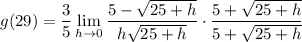
- Multiply:
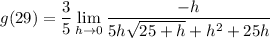
- Factor:
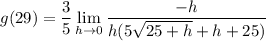
- Simplify:
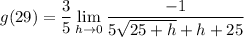
- Evaluate limit [Limit Rule - Variable Direct Substitution]:
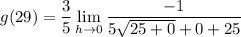
- Simplify:
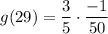
- Multiply:
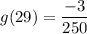
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Derivatives
Book: College Calculus 10e