Answer:
85cm²
Explanation:
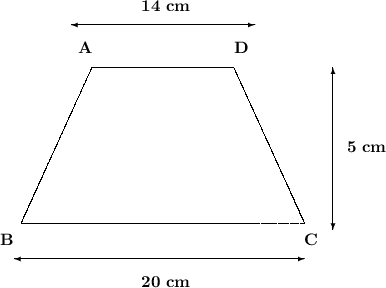
Here we are given a trapezium with base = 20cm and 14cm and height = 5cm . And we are interested in finding the area of the trapezium .
Figure :-
As we know that the area of trapezium is given by ,
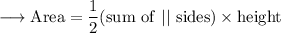
- Here 20cm and 14cm are parallel sides .
Substitute the respective values in stated formula,
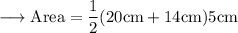
Solve the parenthesis ,
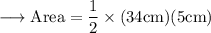
Simplify by multiplying ,
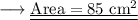
And we are done !
