Question

Please help!! i have no clue what to do and this packet is due tonight.

Answer 1

[D] ∞

General Formulas and Concepts:

Calculus

Limits

Explanation:

Step 1: Define

Identify

`\displaystyle \lim_(n \to \infty) s(n)`

`\displaystyle s(n) = ((5)/(4n^4))(3n^5 + 3n^4 + 2n^3 + n^2)`

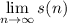
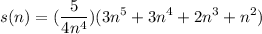
Step 2: Evaluate

1. Substitute in function [Limit]:
   `\displaystyle \lim_(n \to \infty) ((5)/(4n^4))(3n^5 + 3n^4 + 2n^3 + n^2)`
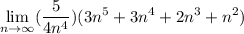
2. Multiply:
   `\displaystyle \lim_(n \to \infty) (5(3n^5 + 3n^4 + 2n^3 + n^2))/(4n^4)`
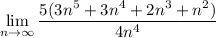
3. Power Method:
   `\displaystyle \lim_(n \to \infty) (5(3n^5 + 3n^4 + 2n^3 + n^2))/(4n^4) = \infty`

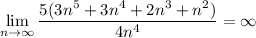
Since the degree of the polynomial is greater in the numerator than in the denominator, the top will always increase faster than the bottom, thus getting infinitely larger.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits

Book: College Calculus 10e