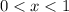Question

Given that y = (e^x)/x, x > 0, find the range of values of x where y is a decreasing

function of x.

Answer 1

The interval for which y is a decreasing function of x is:

`(0, 1)`

Or as an inequality:

`0<x<1`

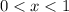
Explanation:

We are given the equation:

`\displaystyle y=(e^x)/(x)\, ,x>0`

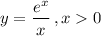
And we want to find the range of values x for which y is a decreasing function of x.

y is decreasing whenever y' is negative. Find y' using the Quotient Rule:

`\displaystyle y'=((e^x)'(x)-e^x(x)')/((x)^2)`

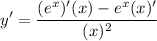
Differentiate:

`\displaystyle y'=(xe^x-e^x)/(x^2)`

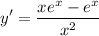
y is decreasing whenever y' is negative. Thus:

`\displaystyle 0>(xe^x-e^x)/(x^2)`

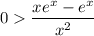
Multiply both sides by x². This is always positive so we do not need to change the sign:

`xe^x-e^x<0`

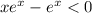
Factor:

`e^x(x-1)<0`

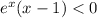
eˣ is always positive. So:

`x-1<0`

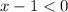
Adding one to both sides produces:

`x<1`

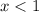
Therefore, y is a decreasing function of x when x is less than one (and greater than 0).

In interval notation:

`(0, 1)`

Or as an inequality:

`0<x<1`