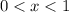Answer:
The interval for which y is a decreasing function of x is:
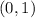
Or as an inequality:
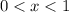
Explanation:
We are given the equation:
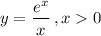
And we want to find the range of values x for which y is a decreasing function of x.
y is decreasing whenever y' is negative. Find y' using the Quotient Rule:
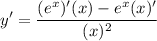
Differentiate:
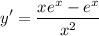
y is decreasing whenever y' is negative. Thus:
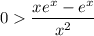
Multiply both sides by x². This is always positive so we do not need to change the sign:
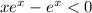
Factor:
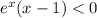
eˣ is always positive. So:
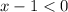
Adding one to both sides produces:
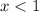
Therefore, y is a decreasing function of x when x is less than one (and greater than 0).
In interval notation:
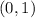
Or as an inequality: