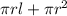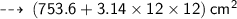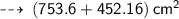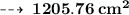Given :
- The height of a cone is 16 cm.
- Its base radius is 12 cm.
⠀
To Find :
- The curved surface area of the cone.
- The total surface area of the cone.
⠀
Solution :
Here,
- h is denoted as height.
- r is denoted as radius.
So, from l² = h² + r², we have :
⠀
- The slang height of the cone is represented by l.
⠀
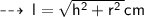
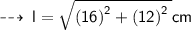
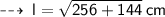
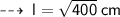
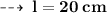
⠀
So, Curved surface area =
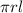
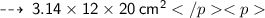
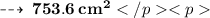
⠀
Further, total surface area =