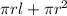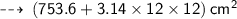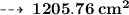Question

the height of a cone is 16 cm and its base radius is 12 cm. find the curved surface area and the total surface area of the cone​

Answer 1

A≈1206.37 cm²

Explanation:

Radius = 12

Height = 16

Using the formulas

A= πrl+πr²

l = √r²+h²

A=πr(r + √h²+r²)=

π·12·(12+√16²+12²) ≈1206.37158cm²

Answer 2

Given :

• The height of a cone is 16 cm.
• Its base radius is 12 cm.

⠀

To Find :

• The curved surface area of the cone.
• The total surface area of the cone.

⠀

Solution :

• h = 16 cm
• r = 12 cm

Here,

• h is denoted as height.
• r is denoted as radius.

So, from l² = h² + r², we have :

⠀

• The slang height of the cone is represented by l.

⠀

`{\qquad \sf \dashrightarrow{ \: l = \sqrt{ {h}^(2) + {r}^(2) \: }cm }}`

`{\qquad \sf \dashrightarrow{ \: l = \sqrt{ {(16)}^(2) + {(12)}^(2) \: }cm }}`

`{\qquad \sf \dashrightarrow{ \: l = √( 256 + 144 ) \: cm }}`

`{\qquad \sf \dashrightarrow{ \: l = √( 400) \: cm }}`

`{\qquad \sf \dashrightarrow{ \: \bf l = 20 \: cm }}`

⠀

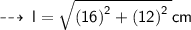
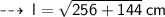
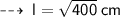
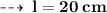
So, Curved surface area =
`\pi{rl}`

`{\qquad \sf \dashrightarrow \: 3.14 * 12 * 20 \: {cm}^(2) }</p><p>`

`{\qquad \bf \dashrightarrow \: 753.6 \: {cm}^(2) }</p><p>`

⠀

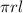
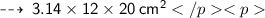
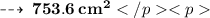
Further, total surface area =
`\pi{rl} + \pi{ {r}^(2) }`

`{\qquad \sf \dashrightarrow \: (753.6 + 3.14 * 12 * 12 )\: {cm}^(2) }`

`{\qquad \sf \dashrightarrow \: (753.6 + 452.16 )\: {cm}^(2) }`

`{\qquad \bf \dashrightarrow \: 1205.76 \: {cm}^(2) }`