Question

A bullet of mass 0.5 kg is moving horizontally with a speed of 50 m/s when it hits a block

of mass 3 kg that is at rest on a horizontal surface with a coefficient of friction of 0.2.
After the collision the bullet becomes embedded in the block.
A) What is the net momentum of the bullet-block system before the collision?
B) Find the total energy of the bullet-block system before the collision?
C) What is the speed of the bullet-block system after the collision?
D) *Find the total energy of the bullet-block system after the collision?
E) *How much work must be done to stop the bullet-block system?
F) *Find the maximum traveled distance of the bullet-block after the collision?

Answer 1

a) The net momentum of the bullet-block system before the collision is 25 kilogram-meters per second.

b) The initial translational kinetic energy of the bullet before the collision is 625 joules.

c) The final speed of the bullet-block system after the collision is 7.143 meters per second.

d) The total energy of the bullet-block system after the collision is 89.289 joules.

e) 89.289 joules must be done to stop the bullet-block system.

f) The bullet-block system will travel 13.007 meters before stopping.

Step-by-step explanation:

a) Since no external forces are applied on the system defined by the bullet and the block, then the net momentum is conserved and can be calculated by the initial momentum of the bullet:

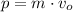`p = m\cdot v_(o)` (1)

Where:

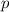`p` - Net momentum, in kilogram-meters per second.

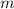`m` - Mass of the bullet, in kilograms.

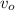`v_(o)` - Initial speed of the bullet, in meters per second.

If we know that
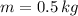`m = 0.5\,kg` and
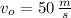`v_(o) = 50\,(m)/(s)`, then the net momentum of the bullet-block system before the collision is:

`p = (0.5\,kg)\cdot \left(50\,(m)/(s) \right)`

`p = 25\,(kg\cdot m)/(s)`

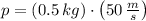
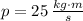
The net momentum of the bullet-block system before the collision is 25 kilogram-meters per second.

b) The total energy of the bullet before the collision is its initial translational kinetic energy (
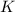`K`), in joules:

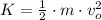`K = (1)/(2)\cdot m \cdot v_(o)^(2)` (2)

`K = (1)/(2)\cdot (0.5\,kg)\cdot \left(50\,(m)/(s) \right)^(2)`

`K = 625\,J`

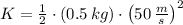
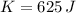
The initial translational kinetic energy of the bullet before the collision is 625 joules.

c) Both the bullet and the block experiments a complete inelastic collision, then the final speed of the bullet-block system is calculated solely by the Principle of Momentum Conservation:

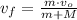`v_(f) = (m\cdot v_(o))/(m+M)` (3)

Where:

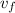`v_(f)` - Final speed, in meters per second.

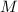`M` - Mass of the block, in kilograms.

If we know that
`m = 0.5\,kg`,
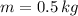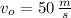`v_(o) = 50\,(m)/(s)` and
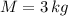`M = 3\,kg`, then the final speed of the bullet-block system is:

`v_(f) = \left((0.5\,kg)/(0.5\,kg + 3\,kg) \right)\cdot \left(50\,(m)/(s) \right)`

`v_(f) = 7.143\,(m)/(s)`

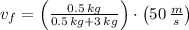
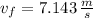
The final speed of the bullet-block system after the collision is 7.143 meters per second.

d) The total energy of the bullet-block system after the collision is the translational kinetic energy of the system (
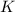`K`), in joules, is:

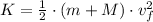`K = (1)/(2)\cdot (m + M)\cdot v_(f)^(2)` (4)

`K = (1)/(2)\cdot (0.5\,kg + 3\,kg)\cdot \left(7.143\,(m)/(s) \right)^(2)`

`K = 89.289\,J`

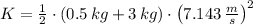
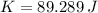
The total energy of the bullet-block system after the collision is 89.289 joules.

e) By Work-Energy Theorem, magnitude of the work done by friction must be equal to the magnitude of the translational kinetic energy of the system. Hence, 89.289 joules must be done to stop the bullet-block system.

f) The maximum travelled distance of the bullet-block after the collision can be determined by means of Work-Energy Theorem and definition of work:

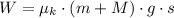`W = \mu_(k)\cdot (m+M)\cdot g\cdot s` (5)

Where:

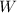`W` - Work done by friction, in joules.

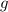`g` - Gravitational acceleration, in meters per square second.

`s` - Travelled distance, in meters.

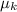`\mu_(k)` - Kinetic coefficient of friction, no unit.

If we know that
`m = 0.5\,kg`,
`M = 3\,kg`,
`\mu_(k) = 0.2`,
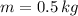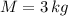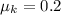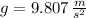`g = 9.807\,(m)/(s^(2))` and
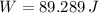`W = 89.289\,J`, then the travelled distance of the bullet-block system is:

`s = (W)/(\mu_(k)\cdot (m+M)\cdot g)`

`s = (89.289\,J)/(0.2\cdot (0.5\,kg + 3\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right))`

`s = 13.007\,m`

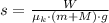
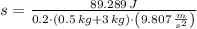
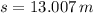
The bullet-block system will travel 13.007 meters before stopping.