Question

Consider this as a simultaneous-move (static) game:

Player B
Left Right
Top 2, 2 3, 2
Player A
Bottom 1, 3 1, 4
1a) Write down the Best Response Correspondence for each of the two players.
1b) Does any player have a dominant strategy in this game? Explain.
1c) Find all Nash Equilibria in pure strategies of this game.
1d) Is there any Nash Equilibria in mixed strategies?

Answer 1

Follows are the solution to the given points:

Explanation:

For point a:

When Player A selects Top, Player B selects Left or Right.

Player B selects Right when player A selects Bottom

Thus, player B's best statement is correct.

When player B selects the left, then game A selects the top

When player B selects the right, player A selects the top

Hence, Player A's right response is Top.

For point b:

The main strategy inside the game is Player A, which would be Top. Since he won't choose Below except under situations since the payment to Bottom is below his payoff for Top irrespective of player B.

For point c:

Player A will purely pick Top & Player B right and player A also will pick Top and player B is right. Game A will's pattern. In this case, neither player has the motive to move away. There are two Nash balances since player B is paid the same amount, irrespective of what he's playing any strategy, as player A is always at the top.

For point d:

Consider if player B plays left with "q" probability and right with "1-q" probability. We're done

`2q + 2(1-q) = 3q+4(1-q) \\\\2(1-q) - 4(1-q) = 3q - 2q \\\\-2(1 - q) = q \\\\-2 + 2q = q \\\\2q-q= 2 \\\\q= 2\\`

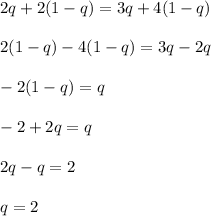
It is not possible since q is a chance that really can exceed 1. Hence, for this game, there is no mixed strategy nash balancing.