Answer:
option E, C
Explanation:
From the graph we will find the equation of g(x).
g(x) is a parabola with vertex ( h, k) = ( 0, 9)
Standard equation of parabola is , y = a (x - h)² + k
y = a (x - 0)² + 9
y = ax² + 9 ---------- ( 1 )
Now we have to find a .
To find a we will take another point through which the parabola passes .
Let it be ( 3, 0).
Substitute ( 3 , 0 ) in ( 1 ) => 0 = a (3 )² + 9
=> - 9 = 9a
=> a = - 1
Substitute a = - 1 in ( 1 ) => y = -1 x² + 9
=> y = - x² + 9
Therefore , g(x) = -x² + 9
Now using the table we will find h(x)
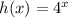
So g(x) = -x² + 9 and
Option A : both function increases on ( 0, ∞ ) - False
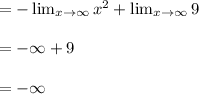
g(x) decreases on ( 0 , ∞)
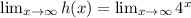

h(x) increases on ( 0, ∞)
option B : g(x) increasing on (- ∞, 0) - False
g(x) = -x² + 9
g( -2 ) = - (-2)² + 9
= - 4 + 9 = 5
g ( -5) = - ( -5)² + 9
= - 25 + 9 = - 14
As the value of x moves towards - ∞ , g(x) moves towards - ∞
Therefore g(x) decreases on (- ∞, 0)
Option C: y intercept of g(x) is greater than h(x) - True
y intercept of g(x) = ( 0 , 9 )
y intercept of h(x) = ( 0 , 1 )
Option D : h(x) is a linear function - False
Option E : g(2) < h(2) - True
g(x) = -x² + 9
g(2) = -(2)² + 9 = - 4 + 9 = 5
h(x) = 4ˣ
h(2) = 4² = 16