Question

For a sixth-order Butterworth high pass filter with cutoff frequency 3 rad/s, compute the following:

a. The locations of the poles.
b. The transfer function H(s).
c. The corresponding LCCDE description.

Answer 1

Given :

A six order Butterworth high pass filter.

∴ n = 6,
`w_c=1 \ rad/s`

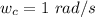
a). The location at poles :

`$s^6-(w_c)^6=0$`

`$s^6=(w_c)^6=1^6$`

∴
`$s^6 = 1$`

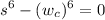
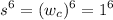
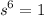
Therefore, it has 6 repeated poles at s = 1.

b). The transfer function H(S) :

Transfer function H(S)
`$=(1)/(1+j\left((w_c)/(s)\right)^6)$`

`$=(1)/(1-\left((w_c)/(s)\right)^6)$`

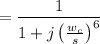
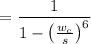
∴ H(S)
`$=(s^6)/(s^6-(w_c)^6)=(s^6)/(s^6-1)$`

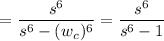
H(S)
`$=(Y(s))/(X(s))=(s^6)/(s^6-1)$`

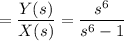
c). The corresponding LCCDE description :

`$=(Y(s))/(X(s))=(s^6)/(s^6-1)$`

`$Y(s)(s^6-1) = s^6 * (s)$`

`$Y(s)s^6-y(s).1 = s^6 * (s)$`

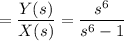
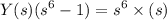
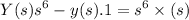
By taking inverse Laplace transformation on BS

`$L^(-1)[Y(s)s^6-Y(s)1]=L^(-1)[s^6 * (s)]$`

`$(d^6y(t))/(dt^6)-y(t)=(d^6 * (t))/(dt^6)$`

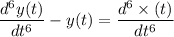
Hence solved.