Solution :
Given :
A six order Butterworth high pass filter.
∴ n = 6,
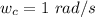
a). The location at poles :
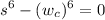
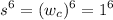
∴
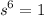
Therefore, it has 6 repeated poles at s = 1.
b). The transfer function H(S) :
Transfer function H(S)
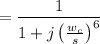
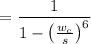
∴ H(S)
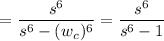
H(S)
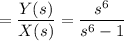
c). The corresponding LCCDE description :
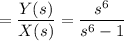
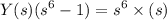
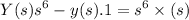
By taking inverse Laplace transformation on BS
![$L^(-1)[Y(s)s^6-Y(s)1]=L^(-1)[s^6 * (s)]$](https://img.qammunity.org/2022/formulas/engineering/college/jr4n3f1rbznkkl2qs9h0b89d1th6galwpu.png)
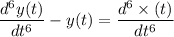
Hence solved.