Question

Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width.4x+y^2=12, x=yThen find the area S of the region.

Answer 1

The Area of the Enclosed Region Is 64/3.

Explanation:

As Given in Question

We have, Curve 4x+
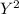`Y^(2)`=12

& X=Y

Solution.

4Y+
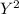`Y^(2)`=12 (X=Y)

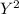`Y^(2)`+4Y-12=0

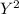`Y^(2)`+6Y-2Y-12=0

Y(Y+6)-2(Y+6)=0

(Y-2)*(Y+6)=0

Y=2 & -6 (X=Y)

Now at (2,2) & (-6,-6) both curves intersect each other.

The Area Of Enclosed Region is
`\int\limits^2_(-6) [(3-Y^(2)/4 )-Y] \, dy`

by Solving This Equation we get Area of Region = 64/3 .

this equation Solution & Curve Diagram please see In Attachment .