Answer:
The Area of the Enclosed Region Is 64/3.
Explanation:
As Given in Question
We have, Curve 4x+
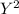 =12
=12
& X=Y
Solution.
4Y+
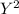 =12 (X=Y)
=12 (X=Y)
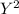 +4Y-12=0
+4Y-12=0
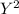 +6Y-2Y-12=0
+6Y-2Y-12=0
Y(Y+6)-2(Y+6)=0
(Y-2)*(Y+6)=0
Y=2 & -6 (X=Y)
Now at (2,2) & (-6,-6) both curves intersect each other.
The Area Of Enclosed Region is
![\int\limits^2_(-6) [(3-Y^(2)/4 )-Y] \, dy](https://img.qammunity.org/2022/formulas/mathematics/college/h92ikc6rwy9httzjn9p3mtcdqssa14697j.png)
by Solving This Equation we get Area of Region = 64/3 .
this equation Solution & Curve Diagram please see In Attachment .