Solution :
a). Let x denotes ACT scores.
ACT scores =
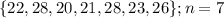
Mean,
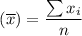
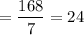
Sample variance,
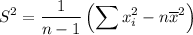
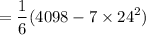
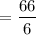
= 11
b). To test whether or not variance of ACT scores of population (say
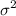 ) of the UTC students is significantly more than 8.
) of the UTC students is significantly more than 8.
Consider the hypothesis :
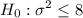 vs
vs
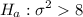
It is a right tailed test and α = 0.05
We have
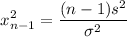
So test statics is
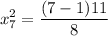
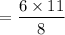
= 8.25
Since our
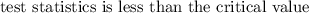 and it falls in a acceptation region, hence we fail to reject
and it falls in a acceptation region, hence we fail to reject
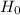 and conclude that variance is not greater than 8 significantly.
and conclude that variance is not greater than 8 significantly.