Question

ACT scores of a sample of UTC students are shown below. Student ACT Score A 22 B 28 C 20 D 21 E 28 F 23 G 26 a. Compute the mean and the variance. B. At 95% confidence, test to determine whether or not the variance of the ACT scores of the population of UTC students is significantly more than 8.

Answer 1

a). Let x denotes ACT scores.

ACT scores =
`$\{ 22,28,20,21,28,23,26 \} ; n = 7$`

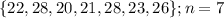
Mean,
`$(\overline x)=(\sum x_i)/(n)$`

`$=(168)/(7)=24$`

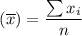
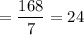
Sample variance,
`$S^2=(1)/(n-1)\left(\sum x_i^2-n\overline x^2 \right)$`

`$=(1)/(6)(4098-7 * 24^2)$`

`$=(66)/(6)$`

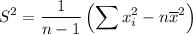
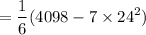
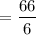
= 11

b). To test whether or not variance of ACT scores of population (say
`$\sigma^2$`) of the UTC students is significantly more than 8.

Consider the hypothesis :

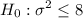`$H_0: \sigma^2 \leq8$` vs
`$H_a: \sigma^2 >8$`

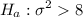
It is a right tailed test and α = 0.05

We have

`$x^2_(n-1) = ((n-1)s^2)/(\sigma^2)$`

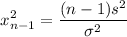
So test statics is

`$x^2_7=((7-1)11)/(8)$`

`$=(6 * 11)/(8)$`

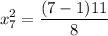
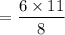
= 8.25

Since our
`\text{test statistics is less than the critical value }`and it falls in a acceptation region, hence we fail to reject
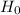`$H_0$` and conclude that variance is not greater than 8 significantly.