Answer: Choice C)
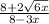
======================================
Work Shown:

This shows why choice C is the answer.
----------------
Notes:
- If you have a+sqrt(b) in the denominator, multiply top and bottom by a-sqrt(b) which is the conjugate, and that will rationalize the denominator.
- In the second step, I multiplied top and bottom by 4+sqrt(6x) to rationalize the denominator
- In step 3, I used the difference of squares rule. In the step afterward, the square root is eliminated.