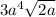Answer:
The answer is
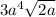
Explanation:
To simplify the radical, start by factoring 9 out of 18 for step 1. Next, for step 2, rewrite 9 as
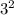 . Then, factor out
. Then, factor out
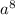 for step 3. For step 4, rewrite
for step 3. For step 4, rewrite
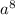 as
as
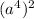 . Then, for step 5, move the 2 in the radical. Rewrite
. Then, for step 5, move the 2 in the radical. Rewrite
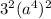 as
as
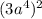 for step 6. Then, add parentheses to the radical for step 7. Finally, for step 8 pull the terms out from under the radical, and the answer is
for step 6. Then, add parentheses to the radical for step 7. Finally, for step 8 pull the terms out from under the radical, and the answer is
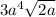 .
.
Step 1:
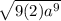
Step 2:

Step 3:
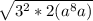
Step 4:
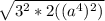
Step 5:
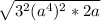
Step 6:
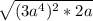
Step 7:
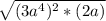
Step 8: