Question

An object is taken from an oven at 350o F and left to cool in a room at 70o F. If the temperature fell to 250o F in one hour, what would its temperature be 4 hours after it was removed from the oven

Answer 1

117.83° F

Step-by-step explanation:

Using Newton's Law of Cooling which can be expressed as:

`(dT)/(dt)= k(T-T_1)`

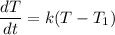
The differential equation can be computed as:

`(dT)/(dt)= k(T-70)`

`(dT)/((T-70))= kdt`

`\int (dT)/((T-70))= \int kdt`

`In|T-70| = kt +C`

`T- 70 = e^(kt+C) \\ \\ T = 70+e^(kt+C) \\ \\ T = 70 + C_1e^(kt) --- (1)`

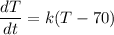
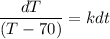
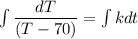
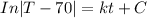
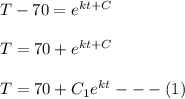
where;

`C_1 = e^C`

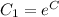
At the initial condition, T(0)= 350

`350 = 70 C_1^(k*0)`

`350 -70 = C_1`

`280 = C_1`

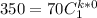
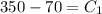
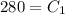
replacing
`C_1`= 280 into (1)

Hence, the differential equation becomes:

`T(t) = 70 + 280 e^(kt)`

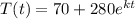
when;

time (t) = 1 hour

T(1) = 250

Since;

`250 = 70 + 280 e^(k*1)`

`180 = 280e^k \\ \\ (180)/(280)= e^k`

`k = In ((180)/(280))`

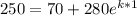
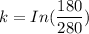
k = -0.4418

Therefore;

T(t) = 70 + 280e^{(-0.4418)}t

After 4 hours, the temperature is:

T(t) = 70 + 280e^{(-0.4418)}4

T(4) = 117.83° F