Answer:
117.83° F
Step-by-step explanation:
Using Newton's Law of Cooling which can be expressed as:
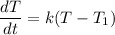
The differential equation can be computed as:
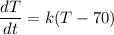
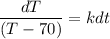
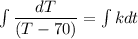
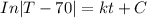
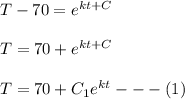
where;
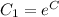
At the initial condition, T(0)= 350
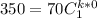
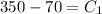
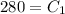
replacing
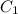 = 280 into (1)
= 280 into (1)
Hence, the differential equation becomes:
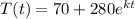
when;
time (t) = 1 hour
T(1) = 250
Since;
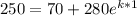
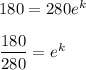
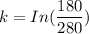
k = -0.4418
Therefore;
T(t) = 70 + 280e^{(-0.4418)}t
After 4 hours, the temperature is:
T(t) = 70 + 280e^{(-0.4418)}4
T(4) = 117.83° F