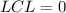Question

Management at Webster Chemical Company is concerned as to whether caulking tubes are being properly capped. If a significant proportion of the tubes are not being​ sealed, Webster is placing its customers in a messy situation. Tubes are packaged in large boxes of . Several boxes are​ inspected, and the following numbers of leaking tubes are​ found: Sample Tubes Sample Tubes Sample Tubes 1 8 15 2 9 16 3 10 17 4 11 18 5 12 19 6 13 20 7 14 Total Calculate​ p-chart ​-sigma control limits to assess whether the capping process is in statistical control.

Answer 1

`UCL = 0.078`

`LCL = 0`

Explanation:

Poorly formatted question (see attachment)

From the attachment, we have:

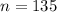`n = 135` --- the sample size

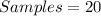`Samples = 20` --- The number of samples

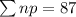`\sum np = 87` --- Number of leaking tubes

First, we calculate the number of observations

`\sum n = n * Samples`

`\sum n= 135 * 20`

`\sum n= 2700`

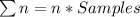
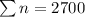
Using 3 sigma control limit, we have:

`z = 3`

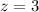
Calculate
`\bar p`

`\bar p = (\sum np)/(\sum n)`

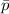
So, we have:

`\bar p = (87)/(2700)`

`\bar p = 0.0322`

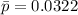
Next, calculate the standard deviation

`s_p = \sqrt{(\bar p* (1-\bar p))/(n)}`

So, we have:

`s_p = \sqrt{(0.0322* (1-0.0322))/(135)}`

`s_p = \sqrt{(0.03116)/(135)}`

`s_p = √(0.0002308)`

`s_p = 0.0152`

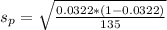
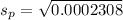
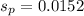
The control limits is then calculated as:

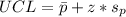`UCL = \bar p + z * s_p` --- upper control limit

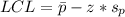`LCL = \bar p - z * s_p` --- lower control limits

So, we have:

`UCL = \bar p + z * s_p`

`UCL = 0.0322 +3 * 0.0152`

`UCL = 0.078`

`LCL = \bar p - z * s_p`

`LCL = 0.0322 - 3 * 0.0152`

`LCL = -0.013`

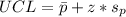
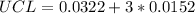
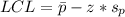
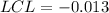
Since the calculated LCL is less than 0, we simply set it to 0

`LCL = 0`

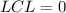
So, the p chart control limits are:

`UCL = 0.078`

`LCL = 0`