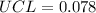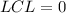Answer:
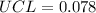
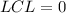
Explanation:
Poorly formatted question (see attachment)
From the attachment, we have:
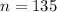 --- the sample size
--- the sample size
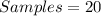 --- The number of samples
--- The number of samples
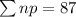 --- Number of leaking tubes
--- Number of leaking tubes
First, we calculate the number of observations
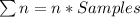
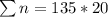
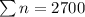
Using 3 sigma control limit, we have:
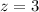
Calculate
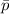
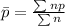
So, we have:
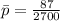
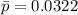
Next, calculate the standard deviation
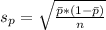
So, we have:
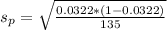
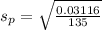
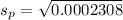
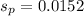
The control limits is then calculated as:
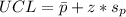 --- upper control limit
--- upper control limit
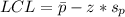 --- lower control limits
--- lower control limits
So, we have:
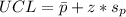
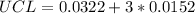
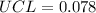
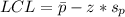
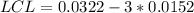
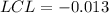
Since the calculated LCL is less than 0, we simply set it to 0
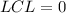
So, the p chart control limits are: