Question

Is this quadratic? If so what form is it?

Answer 1

Yes. Factored form.

Explanation:

Answer 2

yes, and it's in intercept form

Explanation:

Hi there!

We are given the function f(x)=-2(x-4)(x+3)

A quadratic function is a function that has a degree of 2 (the highest exponent in the function is to the 2nd power)

There are 3 forms to write a quadratic function:

standard form, which is f(x)=ax²+bx+c, where a, b, and c are free coefficients (numbers)

vertex form, which is f(x)=a(x-h)²+k, where a is a free coefficient and (h,k) is the vertex

intercept form, which is f(x)=a(x-
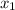`x_(1)`)(x-
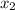`x_(2)`), where a is a free coefficient and
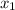`x_(1)` and
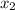`x_(2)` are the x intercepts

You may notice that f(x)=-2(x-4)(x+3) is actually in intercept form; a is -2 and
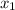`x_(1)` and
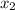`x_(2)` are 4 and -3 respectively (remember: the formula for intercept form has -
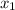`x_(1)` and -
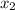`x_(2)`, but the x intercepts are
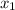`x_(1)` and
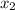`x_(2)`. Therefore, the x intercepts should be the opposites of -
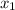`x_(1)` and -
`x_(2)`).

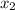If the formula is in intercept form, it should be quadratic.

However, if you want to be sure it's quadratic, you can expand the function.

f(x)=-2(x-4)(x+3)

first, multiply the binomials together using FOIL

(x-4)(x+3)

x²-x-12

now multiply x²-x-12 by -2

-2(x²-x-12)

do the distributive property

-2x²+2x+24

It's a quadratic function! The value of the highest exponent is 2 :)

Hope this helps!