Answer:
After the third bounce the ball reaches a height of less than 50cm.
Explanation:
Geometric sequence:
In a geometric sequence, the quotient between consecutive terms is always the same, and it's called common ratio. The nth term of a geometric sequence is given by:
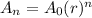
In which
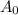 is the first term and r is the common ratio.
is the first term and r is the common ratio.
A ball is dropped from a height of 5m.
This means that
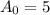
After each bounce it rises to 35% of its previous height.
This means that
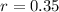
Thus
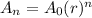
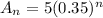
After how many bounces does the ball reach a Height of less than 50cm?
50cm = 0.5m. This is n for which
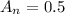 . Thus
. Thus
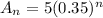
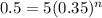
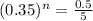
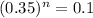
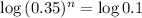
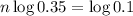
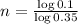
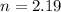
Rounding up:
After the third bounce the ball reaches a height of less than 50cm.