Question

A ball is dropped from a height of 5m. After each bounce it rises to 35% of its previous height. After how many bounces does the ball reach a Height of less than 50cm?

Answer 1

After the third bounce the ball reaches a height of less than 50cm.

Explanation:

Geometric sequence:

In a geometric sequence, the quotient between consecutive terms is always the same, and it's called common ratio. The nth term of a geometric sequence is given by:

`A_n = A_0(r)^(n)`

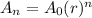
In which
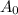`A_0` is the first term and r is the common ratio.

A ball is dropped from a height of 5m.

This means that
`A_0 = 5`

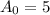
After each bounce it rises to 35% of its previous height.

This means that
`r = 0.35`

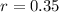
Thus

`A_n = A_0(r)^(n)`

`A_n = 5(0.35)^(n)`

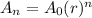
After how many bounces does the ball reach a Height of less than 50cm?

50cm = 0.5m. This is n for which
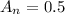`A_n = 0.5`. Thus

`A_n = 5(0.35)^(n)`

`0.5 = 5(0.35)^(n)`

`(0.35)^n = (0.5)/(5)`

`(0.35)^n = 0.1`

`\log{(0.35)^n} = \log{0.1}`

`n\log{0.35} = \log{0.1}`

`n = \frac{\log{0.1}}{\log{0.35}}`

`n = 2.19`

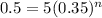
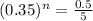
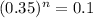
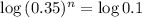
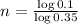
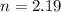
Rounding up:

After the third bounce the ball reaches a height of less than 50cm.