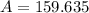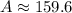Question

How do i solve this problem

Answer 1

`A\approx 159.6`

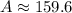
Explanation:

1. Approach

To solve this problem, divide the given figure up into two smaller figures, a rectangle and a semi-circle. Find the area of each figure and add up the values to find the total area. Remember the formula to find the area of a rectangle is as follows (
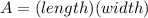`A=(length)(width)`). The formula to find the area of a circle is the following, (
`A=(\pi)(r^2)`).

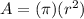2. Find the area of the rectangle

The radius is the measurement in a circle from the center of a circle to any point on the circle's circumference (outer edge). The diameter is a line going through a circle connecting two opposite edges on a circle and passing through the center of a circle. By its definition, the diameter is always twice the radius of a circle.

As one can see in the rectangle, the side of the rectangle is made of the diameter of the circle. Since the diameter of a circle is twice the radius, one must multiply the radius by (2), then multiply that value by the length of the rectangle to find the area of the rectangle,

`A=(length)(width)\\`

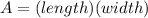
Substitute,

`A_r=(length)(2(radius))\\A_r=(14)(2(5))`

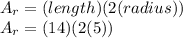
Simplify,

`A_r=(14)(2(5))\\A_r=(14)(10)\\A_r=140`

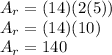
3. Find the area of the semi-cricle

Now one has to find the area of the semi-circle. Since a semi-circle is half of a circle, one must divide the formula to find the area of a circle by (2) in order to find the area of a semi-circle. Remember parameter (r) represents the radius, and (
`\pi`) represents the numerical value (3.1415...)

`A=((\pi)(r^2))/(2)`

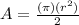
Substitute,

`A_s=((\pi)(5^2))/(2)`

Simplify,

`A_s=((\pi)(5^2))/(2)\\A_s=((\pi)(25))/(2)\\A_s=12.5((\pi))/(2)\\A_s\approx19.635`

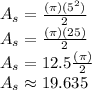
4. Find the total area

To find the total area of the figure, one must add up the two components, add the area of the rectangle to the area of the semi-circle,

`A=A_r+A_s\\`

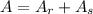
Substitute,

`A=140+19.635`

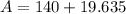
Simplify,

`A=159.635`

`A\approx 159.6`