Question

Look at the image. (calculus)

Answer 1

2

Step-by-step explanation:

`=\frac{\sqrt{1-cos^(2)x }}{sinx} +\frac{\sqrt{1-sin^(2)x } }{cosx} \\\\When \:0 < x < (\pi )/(2) \\\\=\frac{\sqrt{sin^(2)x } }{sinx} +\frac{\sqrt{cos^(2)x } }{cosx} \\\\=(sinx)/(sinx) +(cosx)/(cosx) \\\\=1+1\\\\=2`

Here we use the formula sin²x=1-cos²x and cos²x=1-sin²x.

Answer 2

Answer: Choice H) 2

=============================================

Step-by-step explanation:

Recall that the pythagorean trig identity is
`\sin^2 x + \cos^2x = 1`

If we were to isolate sine, then,

`\sin^2 x + \cos^2x = 1\\\\\sin^2 x = 1-\cos^2x\\\\\sin x = √(1-\cos^2x)\\\\`

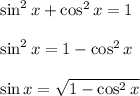
We don't have to worry about the plus minus because sine is positive when 0 < x < pi/2.

Through similar calculations,
`\cos x = √(1-\sin^2x)\\\\`

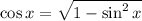
Cosine is also positive in this quadrant.

-------------

So,

`(√(1-\cos^2x))/(\sin x)+(√(1-\sin^2x))/(\cos x)\\\\(\sin x)/(\sin x)+(\cos x)/(\cos x)\\\\1+1\\\\2`

Therefore,

`(√(1-\cos^2x))/(\sin x)+(√(1-\sin^2x))/(\cos x)=2`

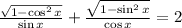
is an identity as long as 0 < x < pi/2