Answer:
<J = 60.26
<L = 28.84
JL =
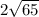
Explanation:
One is given that triangle (JKL) is a right triangle. The measurements for the legs (JK) and (KL) are given; (8) and (14) respectively. One can use the Pythagorean theorem to solve for the unknown side, the hypotenuse. The Pythagorean theorem states the following,
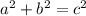
Where (a) and (b) are the legs or sides adjacent to the right angle of the right triangle. (c) is the hypotenuse or the side opposite the right angle of the right triangle. Substitute in the given values and solve for the unknown,
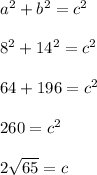
Now one has to find the unknown angles. This can be done using the right triangle trigonometric ratios. These ratios are used to describe the relationship between the sides and an angle of a triangle. These ratios are as follows,
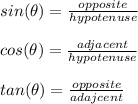
Bear in mind that the sides are named relative to the angle one is describing it from. Thus, the name of the (opposite) and (adjacent) sides change relative to the angle of description. However, the hypotenuse is the side opposite the right angle, this side never changes its name.
Solve for (<J)
Since one has the measures of all of the sides, one can use any ratio. In this case, let's use the ratio of tangent (tan).
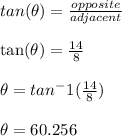
Solve for (<L)
The sum of angles in any triangle is (180) degrees. One can use this property here. Form an equation by adding up all of the angle measures, and solve for (<L)
(<L) + (<J) + (<K) = 180
(<L) + 60.26 + 90 = 180
(<L) + 151.16 = 180
(<L) = 28.84