Question

The Answer to This Question

Answer 1

to nem ai se vc excluiu minha respostpa q soud o5 oa

n

Answer 2

Recall the Trigonometric Ratio below:

`\tt{ \large{sin \theta = (opposite)/(hypotenuse) } }\\ \tt{\large{cos \theta = (adjacent)/(hypotenuse) }} \\ \tt{ \large{tan \theta = (opposite)/(adjacent) }}`

For csc, sec and cot - they are reciprocal of sin,cos and tan.

`\tt{ \large{csc \theta = (1)/(sin \theta) } }\\ \tt{ \large{sec \theta = (1)/(cos \theta) }} \\ \tt{ \large{cot \theta = (1)/(tan \theta) }}`

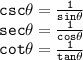
What we know now is our hypotenuse, adjacent and opposite length.

• hypotenuse = 15
• opposite = 12
• adjacent = 9

Therefore,

`\large{sin \theta = (12)/(15) \longrightarrow (4)/(5) } \\ \large{cos \theta = (9)/(15) \longrightarrow (3)/(5) } \\ \large{ tan \theta = (12)/(9) \longrightarrow (4)/(3) }`As for the reciprocal of three trigonometric ratio. We just swap the numerator and denominator.

`\large{csc \theta = (15)/(12) \longrightarrow (5)/(4) } \\ \large{sec \theta = (15)/(9) \longrightarrow (5)/(3) } \\ \large{cot \theta = (9)/(12) \longrightarrow (3)/(4) }`

Answer

• sin = 12/15 —> 4/5
• cos = 9/15 —> 3/5
• tan = 12/9 —> 4/3
• csc = 15/12 —> 5/4
• sec = 15/9 —> 5/3
• cot = 9/12 —> 3/4

The first is non-simplifed form while the second that has the arrow pointing is the simplest form.

Let me know if you have any doubts.