Question

The coordinates of the endpoints of BC are B(5,1) and (-3,-2). Under the

transformation R90, the image of BC is B'C". State the coordinates of points B
and C.

Answer 1

Given:

The coordinates of the endpoints of segment BC are B(5,1) and (-3,-2).

Under the transformation
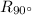`R_(90^\circ)` the image of
`\overline{BC}` is
`\overline{B'C'}`.

To find:

The coordinates of points B' and C'.

Solution:

We know that transformation
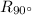`R_(90^\circ)` means 90 degrees counterclockwise rotation about the origin.

If a figure is rotated 90 degrees counterclockwise rotation about the origin, then

`(x,y)\to (-y,x)`

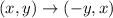
Using this rule, we get

`B(5,1)\to B'(-1,5)`

Similarly,

`C(-3,-2)\to C'(-(-2),-3)`

`C(-3,-2)\to C'(2,-3)`

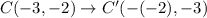
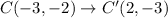
Therefore, the coordinates of required points are B'(-1,5) and C'(2,-3).