Given:
The coordinates of the endpoints of segment BC are B(5,1) and (-3,-2).
Under the transformation
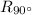 the image of
the image of
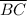 is
is
 .
.
To find:
The coordinates of points B' and C'.
Solution:
We know that transformation
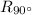 means 90 degrees counterclockwise rotation about the origin.
means 90 degrees counterclockwise rotation about the origin.
If a figure is rotated 90 degrees counterclockwise rotation about the origin, then
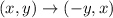
Using this rule, we get
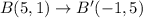
Similarly,
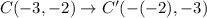
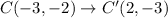
Therefore, the coordinates of required points are B'(-1,5) and C'(2,-3).