Question

Which property allows to compute [(-1/5) + (-3/5)] + (1/7) as (-1/5) + [(-3/5) + (1/7)]

Answer 1

Given:

Two expressions are
`\left[\left(-(1)/(5)\right)+\left(-(3)/(5)\right)\right]+\left((1)/(7)\right)` and
`\left(-(1)/(5)\right)+\left[\left(-(3)/(5)\right)+\left((1)/(7)\right)\right]`.

To find:

The property that allows to compute
`\left[\left(-(1)/(5)\right)+\left(-(3)/(5)\right)\right]+\left((1)/(7)\right)` as
`\left(-(1)/(5)\right)+\left[\left(-(3)/(5)\right)+\left((1)/(7)\right)\right]`.

Solution:

According to associative property of addition, if a, b and c are real numbers, then

`(a+b)+c=a+(b+c)`

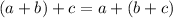
Using the associative property of addition, we get

`\left[\left(-(1)/(5)\right)+\left(-(3)/(5)\right)\right]+\left((1)/(7)\right)=\left(-(1)/(5)\right)+\left[\left(-(3)/(5)\right)+\left((1)/(7)\right)\right]`

Therefore, the required property is associative property of addition.