Answer:
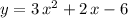 .
.
Explanation:
In general, the equation of a parabola is in the form
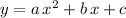 for some constants
for some constants
 ,
,
 , and
, and
 , where
, where
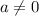 .
.
Let
 denote the equation of this parabola for some constants
denote the equation of this parabola for some constants
 ,
,
 , and
, and
 where
where
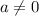 . A point
. A point
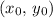 is on this parabola if and only if the equation of this parabola holds after substituting in
is on this parabola if and only if the equation of this parabola holds after substituting in
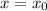 and
and
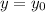 :
:
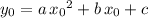 .
.
Thus, each of the three distinct points on this parabola would give a equation about
 ,
,
 , and
, and
 :
:
- The equation for
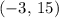 would be
would be
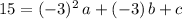 .
. - The equation for
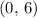 would be
would be
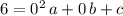 .
. - The equation for
 would be
would be
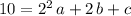 .
.
Simplify the equations:
 .
.
Solve this linear system of three equations and three unknowns for
 ,
,
 , and
, and
 :
:
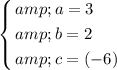 .
.
Therefore, the equation of this parabola would be:
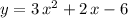 .
.