Answer:
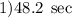
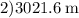
Explanation:
Question-1:
so when flash down occurs the rocket will be in the ground in other words the elevation(height) from ground level will be 0 therefore,
to figure out the time of flash down we can set h(t) to 0 by doing so we obtain:
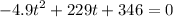
to solve the equation can consider the quadratic formula given by
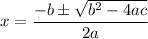
so let our a,b and c be -4.9,229 and 346 Thus substitute:

remove parentheses:
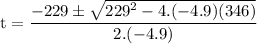
simplify square:

simplify multiplication:
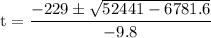
simplify Substraction:

by simplifying we acquire:
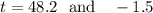
since time can't be negative
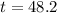
hence,
at 48.2 seconds splashdown occurs
Question-2:
to figure out the maximum height we have to figure out the maximum Time first in that case the following formula can be considered
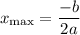
let a and b be -4.9 and 229 respectively thus substitute:
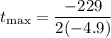
simplify which yields:
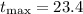
now plug in the maximum t to the function:
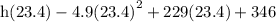
simplify:
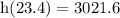
hence,
about 3021.6 meters high above sea-level the rocket gets at its peak?