Question

A random sample of 10 college students was drawn from a large university. Their ages are 22, 17, 27, 20, 23, 19, 24, 18, 19, and 24 years, with a sample standard deviation of 3.2. Suppose that you want to test whether the population mean age differs from 20. What is your decision based on a test at a 1% significance level

Answer 1

Given :

The sample mean = 21.3

Standard deviation = 3.2

The null hypothesis is :
`H_0: \mu =20`

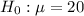
The alternate hypothesis :
`H_a:\mu \\eq20`

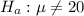
This is a two tailed test, for which a
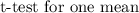`\text{t-test for one mean}` with an unknown population of a standard deviation is being used.

Now the significance level,
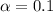`\alpha = 0.1`, as well as the critical value for a two tailed test is
`t_c = 1.833`

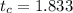
The rejection region is
`R = \ > 1.833 \`

The t-statistic is computed as follows :

`t=(\overline x - \mu_0)/(s/ \sqrt n)`

`t=(21.3-20)/(3.2/ √(10))`

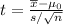
= 1.285

Since it is observed that
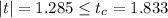`|t| = 1.285 \leq t_c=1.833`, it is then concluded that
`\text{the null hypothesis is not rejected.}`

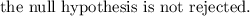
The p-value is p=0.231 and since p 0.231 ≥ 0.1, it is concluded that
`\text{the null hypothesis is not rejected.}`

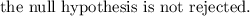
Conclusion

Thus we concluded that
`\text{null hypothesis}`
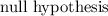
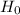`H_0` is not rejected. Therefore, the population mean
`\mu` is different than 20, at the 0.1 significance level.