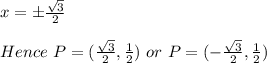Answer:
The answer is below
Explanation:
A unit circle is a circle on the coordinate plane with a radius of 1 unit. The unit circle center usually lies on the origin.
The equation of a circle is given as:
(x - h)² + (y - k)² = r²
Where (h, k) is the center of the circle and r is the radius of the circle.
As seen in the diagram attached, the center of the circle is at the origin (0, 0) and the circle is a unit circle with a radius of 1. Hence:
(x - h)² + (y - k)² = r²
(x - 0)² + (y - 0)² = 1²
x² + y² = 1
Given the point P(x, 1/2) lies on the circle. To find x, substitute y = 1/2:
x² + (1/2)² = 1
x² + 1/4 = 1
x² = 1 - 1/4 = 3/4
x² = 3/4
x = √(3/4)